統計の世界では「サンプル数30」がひとつの基準としてよく使われます。
アンケート調査やABテストなど、ビジネスの現場でも耳にする数字ですが、なぜ 30 なのかを深く説明できる人は意外に多くありません。

この記事では、サンプル数30が特別視される理由を、統計初心者でも理解できるよう丁寧に解説します。
さらに、30では足りないケース、実務でのサンプルサイズ設計の方法、分野ごとの違いまで網羅的に説明し、「サンプル数の考え方」を体系的に学べます。

▼アンケートを正しく効率的に行うならformrun
統計分析やサンプル数設計の前に、「データの集め方」が整っていなければ、どれだけ丁寧に分析しても正しい判断につながりません。

formrun（フォームラン）なら、専門知識がなくてもセキュアで高品質なフォームをすぐに作成でき、回答データは安全に自動収集・整理されます。SSL/TLS通信・ISMS取得・Pマーク取得といった厳格なセキュリティ体制が整っているため、個人情報を扱うアンケートや調査でも安心。
EFO（入力補助）機能によって回答者の離脱を防ぎ、精度の高いデータを集められる点も特徴です。

フォーム作成からデータ管理、メール送信まで一元化できるため、小規模調査から本格的な統計分析まで幅広く活用できます。

最初に、サンプル数30が基準とされる理由を簡潔にまとめます。

• 中心極限定理により平均値が正規分布に近づく境界だから
• t分布と正規分布の差が30付近で急激に小さくなるから
• 実務的にも“精度とコストのバランス”が良い経験則だから

この3つが重なることで、サンプル数30は研究・実務の両方で広く採用されてきました。

サンプル数30が「特別」だと言われる最も重要な理由は、統計学の基本定理である中心極限定理（Central Limit Theorem）にあります。

中心極限定理とは、「サンプル数が増えるほど、標本平均の分布が元の分布の形に関係なく正規分布に近づくという法則」です。

例えば売上のような偏った分布でも、平均をとったときの分布はサンプル数が増えるほど滑らかになっていきます。データのもともとの形が少し歪んでいても、平均値の分布は「きれいな山型」に近づいてくるイメージです。

【図解】サンプル数による標本平均の分布の変化

　　n=5         　　　　n=15              　　　　n=30
□■□■□       □■■□□□■□       ■■■■■■■■■■■
歪んでいる     　　やや歪んでいる      　　正規分布に非常に近い

少ないサンプルだと「たまたま偏ったデータを引いてしまう」可能性が高くなり、平均値が大きくぶれてしまいます。サンプル数が増えると、たまたまのブレが平均化されていき、全体の特徴をより正しく捉えられるようになります。

▼【計算例】標準誤差（SE）の減少で平均値が安定する

標本平均のばらつきは「標準誤差（SE）」という指標で表されます。式は次のとおりです。

SE = σ / √n

ここで、σ（シグマ）は母標準偏差、nはサンプル数です。

母標準偏差 σ＝10 とすると、次のようになります。

サンプル数が10から30に増えるだけでも、標準誤差は大きく減っています。
n＝30付近になると、平均値のブレがかなり小さくなり、「だいたいこの辺が本当の平均だろう」と安心して言いやすくなるイメージです。

こうした性質は Laplace（1810）などの研究者によって古くから確認されており、「30前後は統計的に扱いやすい」という経験則が積み重なってきました。

サンプル数が少ないとき、平均値の推定や検定では「t分布」を使います。

t分布は、正規分布に比べて両端（裾）が少し広がった形をしており、「データにまだ不確実性が大きい」ことを表しています。

しかし、サンプル数が増えると t分布は徐々に正規分布に近づいていきます。

▼【図解】自由度と分布の関係

　df=5      　df=10      　　df=30     　　 df=∞（正規分布）
裾が広い     やや広い      ほぼ一致      完全一致

ここで df（自由度）は、おおまかに「サンプル数−1」と考えて問題ありません。

df=30 付近になると、t分布と正規分布の違いはほとんど目で見てもわからないレベルになります。

この結果として、

• 正規分布用の簡単な計算式や表をそのまま使える
• 推定や検定の手間が減る
• 説明もしやすくなる

といったメリットが得られます。

t分布を用いた「t検定」を発表したのは、ビール会社で品質管理の研究をしていた William S. Gosset（ペンネーム：Student）です。彼の1908年の論文でも、小さいサンプルを扱う際の分布の違いが詳しく議論されており、そこから「30前後」という基準も広く認知されるようになっていきました。

サンプル数30が、統計理論だけでなく現場でも好まれるのには、次のような実務的な事情もあります。

• 調査にかかる時間・コストを抑えられる
• 「さすがに少なすぎる」とは言われにくいライン
• 過去の調査や他社の事例とも比較しやすい
• 仮説検証やパイロット調査の“第一歩”として妥当

特にビジネスの世界では、「完璧な精度」より「意思決定に使える最低限の確からしさ」が求められる場面も多くあります。そうしたときに、 サンプル数30は「とりあえずやってみる」ための現実的な選択肢としてちょうどよいのです。

ただし、繰り返しになりますが、これは「30あれば十分」という意味ではありません。
30はあくまでスタートラインであり、目的や求める精度によってはもっと多くのデータが必要になります。

ここからは、サンプル数30では明らかに不足してしまう代表的なケースを紹介します。
実務では、こちらに該当するかどうかを意識しておくことが大切です。

たとえば、LPのABテストでクリック率0.2%分の差を検出したいとします。
このような「ごく小さな差」を正しく判定するには、n=30ではまったく足りません。

差が小さいほど、偶然のブレと見分けるのが難しくなり、必要なサンプル数は一気に増えていきます。
このようなケースでは、 数百〜数千件単位のデータを集めることが一般的です。

売上、アクセス数、SNSのインプレッション数などは、一部の値だけ飛び抜けて大きかったり、ロングテール構造を持っていたりします。

このようなデータでは、サンプル数が少ないと外れ値の影響を強く受けてしまい、平均値が本当の傾向を反映しにくくなります。

サンプル数30では、たまたま「異常な日」や「バズった投稿」に引きずられた結果になってしまうリスクが高いと言えます。

回帰分析や機械学習モデルでは、説明変数（特徴量）の数に応じて必要なサンプル数が増えます。
よく使われる目安は、次のようなものです。

必要サンプル数 ≧ 説明変数の10倍

例えば説明変数が10個あるモデルであれば、少なくとも100件以上、できればそれ以上のサンプル数が欲しくなります。

変数が多いのにサンプルが少ないと、モデルが「データに過剰適合してしまう（オーバーフィッティング）」リスクも高まります。

男女、年代、居住地、利用プランなど、母集団の属性が幅広い場合も注意が必要です。
全体で30件あっても、属性ごとに分けると「各グループに数件しかない」ということがよく起こります。

このような状況では、「全体の平均」は分かっても、「各属性ごとの違い」や「セグメント別の傾向」を見ることができません。

多様な母集団を代表するには、各層で一定数のサンプルを確保する必要があり、30件ではとても足りない場合が多いのです。

ここでは、実際にサンプル数を決めるときの考え方を、初心者向けに3ステップでまとめます。

▼ アンケート調査で必要なサンプル数を基礎から押さえたい方は、「アンケートのサンプルサイズの基本的な考え方」をこちらで詳しく解説しています。
>>サンプルサイズ 計算方法をやさしく解説｜信頼できるアンケート設計が今日からできる実践ガイド

まずは「結果の誤差をどれくらいまで許容できるか」を決めます。

• 平均値の誤差が±5％までならOKなのか
• もっと精度を高くして±3％にしたいのか

この許容誤差を厳しくするほど、必要なサンプル数は大きくなります。
「どこまで精度を求めるか」を先に決めておくと、サンプル数の議論がしやすくなります。

信頼度とは、「結論がたまたまの誤差でひっくり返ってしまう確率をどこまで抑えるか」を表す指標です。

多くの調査や論文で使われるのは 95%信頼区間で、「100回調査すると95回くらいはこの範囲に本当の値が入るだろう」というイメージです。

信頼度を90% → 95% → 99%と高く設定するほど、「慎重な判断」になりますが、その分だけ必要なサンプル数も増えていきます。

どの程度のリスクを許容するかによって、適切な信頼度を選びましょう。

効果量とは「差の大きさ」、検出力とは「差が本当にあるときに、それを正しく検出できる確率」です。

統計の世界では、 検出力80%以上がひとつの目安とされています。

• 効果量が大きい → 少ないサンプルでも差を見つけやすい
• 効果量が小さい → 多くのサンプルが必要

ABテストや施策の比較実験では、この効果量と検出力を考えずに「とりあえず30だけ集める」としてしまうと、ほとんど何も分からないまま終わってしまうこともあります。

サンプル数が30未満だからといって、何もできないわけではありません。
小規模なデータでも、以下のような工夫で分析の質を高められます。

• ノンパラメトリック検定
  • データが正規分布している前提を置かない検定手法です。
  • 順位や中央値を扱うため、外れ値や偏りのあるデータにも比較的強いのが特徴です。
• ブートストラップ（再サンプリング）
  • 手元のデータから何度もランダムにサンプルを取り直し、統計量の分布を推定する方法です。
  • 理論式に頼らず、コンピュータの計算力で「不確実性」を評価できます。
• 外れ値の確認とロバストな指標の利用
  • 平均だけでなく、中央値や四分位数なども見ることで、外れ値の影響を軽減できます。
  • 外れ値を除外するかどうかの判断も重要なステップです。
• パイロット調査の実施
  • 最初は小規模に調査して、ばらつきや回答傾向を確認し、その結果から本調査のサンプル数を計算する方法です。
  • 無駄な大規模調査を避けつつ、必要十分なサンプル数を見積もるのに役立ちます。

サンプル数30は、あくまで「多くの分野でよく使われる共通の目安」であり、実際に必要な数は分野ごとに大きく違います。

医学研究では、人の健康や安全に関わるため、慎重な判断が求められます。

• 初期段階のパイロット試験や予備調査では、30件前後の小規模な研究もあります。
• 一方で、薬の効果や副作用を本格的に検証する臨床試験では、数百〜数千人規模のサンプル数が必要になることも一般的です。

心理学の実験では、実験室で行う小規模な研究も多く、30件程度のサンプル数で実施される研究も珍しくありません。

しかし近年は「再現性の危機」と呼ばれる問題が注目されており、もっと多くのサンプルを集めて、頑健な結論を導くべきだという意見が強まっています。

マーケティングの調査では、目的に応じて必要なサンプル数が変わります。

• 新しい施策や商品の「手応え」をざっくり確認する初期フェーズでは、30件でもある程度の方向性を掴めます。
• しかし、性別・年代・地域別など、セグメントごとの傾向を分析したい場合は、各セグメントで十分な件数が必要になるため、トータルで数百〜数千件のサンプルが必要になることも多いです。

▼ 集めたアンケート結果をどのように施策や改善に活かすかについては、こちらの記事で具体的な活用方法をまとめています。
>>マーケティングにおけるアンケートの役割は？設計のコツや実施手順、3つの注意点を解説

AIやIoTの分野では、モデルの学習や異常検知の精度を高めるために、大量のデータが求められます。

• 初期検証やプロトタイプ構築の段階では、30件前後のデータからスタートすることもあります。
• しかし、実運用で安定した性能を発揮するためには、 数千〜数万件規模のデータが必要になるケースがほとんどです。

統計分析を正しく行うためには、サンプルサイズ設計だけでなく、「どんな環境でデータを集めるか」も重要な要素です。

フォームの設計が不適切だったり、回答データに偏りや欠損が多いと、どれだけ高度な手法を使っても正確な結論には到達できません。

特に個人情報を含むアンケートや調査では、セキュリティ・入力しやすさ・集計しやすさの3つが不可欠です。

そこで役立つのが、 ノーコードで高品質なフォームを作成できるうえに、セキュリティと操作性も兼ね備えた formrun（フォームラン）です。

統計分析で扱うデータは、アンケート回答や個人情報を含むことも多く、フォーム段階でのセキュリティは欠かせません。

formrun（フォームラン）では、ISO 27001（ISMS）の認証取得やプライバシーマークの付与認定、SSL/TLSによる暗号化通信、24時間監視など、研究・調査用途にも耐えうる堅牢なセキュリティ対策が整っています。

特に、無料ツールでは漏洩リスクが懸念される個人属性データやセンシティブ情報も、formrunなら安全に収集・管理が可能。

“信頼できるデータ”を得るためには、まず安全な収集基盤を確保することが重要です。
セキュリティを重視したい調査・研究担当者におすすめできる環境です。

統計分析では、必要なサンプル数を確保できるかどうかが結果の精度を左右します。しかし、入力エラーや項目の多さによる途中離脱が多いと、実質的なサンプル数は大きく減少してしまいます。

formrunでは、残項目数の可視化、ページ分割、入力途中保存、リアルタイムエラー表示など、回答者がストレスなく最後まで入力しやすいEFO機能を標準搭載。これにより、サンプルの欠損・誤入力・離脱を大幅に抑え、統計分析に使える“質の高いデータ”を確保できます。

一般的に外部EFOツールは導入に3万円ほどかかりますが、formrunなら初期費用ゼロ・月額3,000円〜利用可能。ノーコードで作ったフォームにもこれらの機能が組み込まれているため、コストを抑えつつ必要サンプル数を確保したい調査にも最適です。

EFO機能で回答率を改善し、分析可能なデータを増やした事例も多数あります。
>メールアドレスの入力ミスがほぼゼロに！formrunの入力補助機能を活用した事例（Vollmond株式会社様）

統計分析では、データの収集だけでなく「集計作業にかかる工数」も大きな負担になります。特に、回答データをスプレッドシートへ転記したり、グラフを作り直したりする作業は、分析前の準備として時間がかかりがちです。

formrun（フォームラン）では、ノーコードで作成したフォームの回答内容をリアルタイムで自動集計し、一覧表やグラフを自動生成。分析に必要な基本統計量がすぐに揃うため、表やグラフを手作業で作る必要がありません。キャプチャを貼るだけで社内共有が完結するほど、集計の効率が向上します。

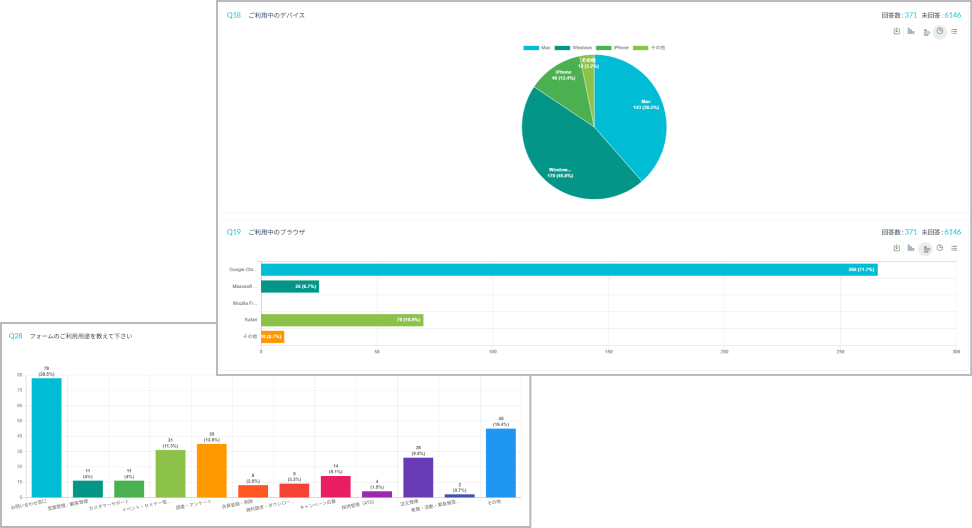
さらに、Googleスプレッドシート連携やExcel出力にも対応。より高度な分析（回帰分析・セグメント分析など）に進む際もスムーズです。集計の手間を最小限にし、本来の分析に時間を使いたい方に最適です。

14日間の無料トライアルならアンケートの自動回答まで完結します。以下のボタンからぜひ、アンケートの集計の簡単さを実感してみてください。

ここまで見てきたように、サンプル数30は次のような意味を持つ目安です。

• 中心極限定理により、平均値の分布が正規分布に近づき、推定が安定し始める
• t分布と正規分布の差が小さくなり、計算や解釈が簡単になる
• 実務的にも、コストと精度のバランスが良く、初期調査のスタートとして使いやすい

しかし同時に、 サンプル数30は「万能の正解」ではなく、“統計手法を無理なく使い始められる最低限のライン”に過ぎません。

分析の目的、許容できる誤差、信頼度、効果量、データのばらつきや構造などを踏まえて、必要なサンプル数を柔軟に設計していくことが大切です。

▼信用性高いアンケート結果を得るならformrunがおすすめ
formrun（フォームラン）を使えば、アンケート・申込み・調査フォームをノーコードで作成でき、回答データは自動で一覧化され、必要に応じてExcelやスプレッドシートへ出力して分析に活用できます。

セキュリティも国内トップレベルで、ISMSやPマーク取得、24時間監視体制など、個人情報を扱うフォーム運用でも安心して利用可能です。

さらに、入力途中保存・リアルタイムエラー表示などのEFO機能により、回答率を高めながら「偏りの少ないデータ」を取得できます。

調査結果を即メールで共有したり、回答者ごとに対応ステータスを管理したりと、運用効率も大きく改善。

正確なサンプル数と信頼できるデータを集めたい方にとって、formrunは最適な基盤となるはずです。

サンプル数30は、中心極限定理やt分布と正規分布の関係から「統計的に扱いやすさが大きく向上する目安」としてよく使われている数字です。

ただし、29がダメで30ならOKというような“魔法の境界”があるわけではなく、あくまで「30前後」が一つの実用的な目安として定着していると考えるのが自然です。

現場では、29と30、30と50の差よりも、「そもそも目的に対してサンプル数が足りているかどうか」の方が重要です。

「30を超えたから安心」ではなく、求める精度や分析内容に対して十分かどうかを、別途検討することが大切です。

いいえ、サンプル数が30未満でも分析は可能です。ただし、サンプル数が少ないほど結果のブレが大きくなり、「たまたま偏ったデータを引いてしまっただけ」というリスクが高くなります。

そのため、結論を出すときには慎重さが求められますし、「傾向の仮説を立てる段階」と割り切って使う方が安全です。

小規模サンプルでも、ノンパラメトリック検定やブートストラップなど、少ないデータに強い手法を使うことで、ある程度信頼性のある結果を得ることもできます。

ただし、最終的な意思決定に使う場合は、後でサンプル数を増やして検証することを強くおすすめします。

割合（例えば「購入した人の割合」や「クリックした人の割合」など）を扱う場合でも、サンプル数30は一つの目安になります。

二項分布を正規分布で近似して計算したいとき、成功数・失敗数がそれぞれある程度多い方が近似の精度が高くなり、その目安として「各カテゴリで30件程度」といった基準が使われることがあります。

ただし、割合の場合は「全体のサンプル数」だけでなく、「成功数・失敗数のどちらにも十分な件数があるか」が重要です。

例えば、100件中1件だけ成功のような極端なケースでは、たとえ全体のサンプルが多くても、通常の正規近似では精度が不十分になることがあります。

多くの場合、ABテストでサンプル数30は全く足りません。特に、クリック率やコンバージョン率のような指標で小さな差を見極めたい場合、サンプル数が30では「たまたまの誤差」と本当の差を区別することがほとんどできません。

その結果、「Aの方が良さそうに見えたけれど、実は運が良かっただけだった」といった誤った判断につながるリスクが高まります。

ABテストでは、期待する効果の大きさ（効果量）と、許容する誤差、検出力（差を見逃さない確率）から必要サンプル数を計算することが重要です。

多くの実務ケースでは、少なくとも数百〜数千件規模のサンプルが必要になることが多いため、「とりあえず30」という発想は避けた方が安全です。

外れ値が多いデータでは、サンプル数が30あっても平均値が大きく歪められてしまうことがあります。例えば、一部の顧客だけが極端に高い金額を使っている売上データなどが典型的な例です。

こうした場合、単純な平均値だけを見て判断すると、「実際の大多数の顧客とは違う姿」を平均が表してしまう可能性があります。

そのため、外れ値が疑われるデータでは、中央値や四分位数、箱ひげ図などを併用し、データの分布全体を確認することが大切です。

必要に応じて、外れ値を除外した分析や、ロバスト統計と呼ばれる外れ値の影響を受けにくい手法を検討することで、より現実に近い判断がしやすくなります。

回帰分析では、「説明変数の数」に対して十分なサンプル数が必要です。一般に使われるシンプルな目安は「説明変数の10倍以上のサンプル数が必要」というものです。

例えば、説明変数が10個ある回帰モデルなら、最低でも100件のサンプルが欲しくなります。

サンプル数が少なすぎると、モデルが手元のデータに過剰に合わせてしまう「オーバーフィッティング」が起こりやすくなり、新しいデータに対して予測性能が落ちてしまいます。

精度の高いモデルを作るには、サンプル数を十分に確保するだけでなく、不要な変数を絞り込むことも重要です。

サンプル数の計算は専門的に聞こえますが、最近はオンラインツールや専用ソフトが充実しており、基本的な考え方さえ押さえれば、初心者でも自分で試算できます。

もちろん、厳密な設計が必要な研究や大きな投資判断に関わるプロジェクトでは、統計の専門家に相談するのが理想的です。

一方で、日常的なABテストや社内の簡易調査であれば、ツールを使って「おおよその目安」を押さえるだけでも、感覚で決めるよりずっと質の高い意思決定ができるようになります。

▼ 実際にアンケート分析で必要なサンプルサイズを計算するステップは、こちらの記事で具体的な手順と例を交えて紹介しています。
>>アンケート サンプル数 計算｜標本誤差・信頼度からわかる適切な有効回答数の目安とは?